1724. Counting
Triangles
We define the LEVEL of a
triangle as in the following illustrative image:
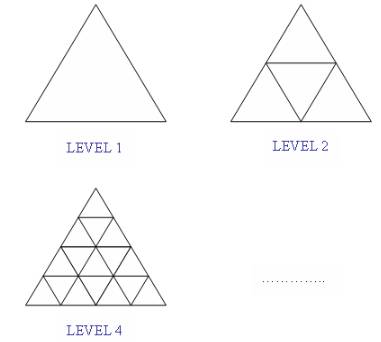
Your task is very easy.
All you have to do is to count all triangles in the biggest one (level n).
Input. The first line of the input contains an integer t (t
≤ 10000) - the number of test cases and t lines follow. Each line contains an integer n (1 ≤ n ≤ 106)
which is the level of the triangle in that test case.
Output. For each test case, you should write a seperate line: the
number of triangles in the biggest one (level n). (All answers will fit within the range of a 64-bit integer)
|
Sample
input |
Sample
output |
|
3 1 2 3 |
1 5 13 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
Рассмотрим ряд
треугольников:
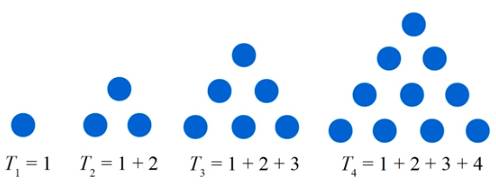
Обозначим через Tn количество точек в нем (назовем Tn треугольными
числами). По сумме
арифметической прогрессии Tn = n (n + 1) / 2.
Подсчитаем
сначала количество треугольников ![]() с вершиной вверх. Каждая
жирная точка на исходном треугольнике является вершиной некоторого меньшего
треугольника.
с вершиной вверх. Каждая
жирная точка на исходном треугольнике является вершиной некоторого меньшего
треугольника.
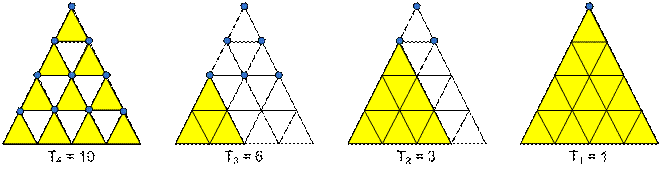
Количество треугольников со
стороной 1 равно Tn.
Количество треугольников со
стороной 2 равно Tn-1.
…
Количество треугольников со
стороной n равно T1.
Итого ![]() = Tn + Tn-1 + Tn-2 + … + T2 + T1 или
= Tn + Tn-1 + Tn-2 + … + T2 + T1 или ![]() = Tn +
= Tn + ![]() .
.
Теперь
подсчитаем количество треугольников ![]() с вершиной вниз.
с вершиной вниз.
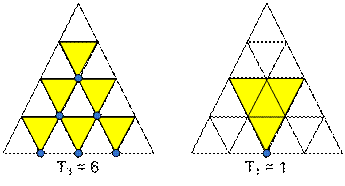
Количество треугольников со
стороной 1 равно Tn-1.
Количество треугольников со
стороной 2 равно Tn-3.
Количество треугольников со
стороной 3 равно Tn-5.
…
Количество треугольников со
стороной n равно 0.
Для четного n имеем: ![]() = Tn-1 + Tn-3 + … + T3 + T1.
= Tn-1 + Tn-3 + … + T3 + T1.
Для нечетного n имеем: ![]() = Tn-1 + Tn-3 + … + T4 + T2.
= Tn-1 + Tn-3 + … + T4 + T2.
Или ![]() = Tn-1 +
= Tn-1 + ![]() .
.
Реализация алгоритма
#include <stdio.h>
#define MAX 1000010
int tests, i;
long long n;
long long s[MAX][2];
long long T(long long n)
{
return n * (n + 1) / 2;
}
int main(void)
{
s[1][0]
= 1; s[2][0] = 3;
s[1][1] = 0; s[2][1] = 1;
for(i = 2; i < MAX; i++)
{
s[i][0] = s[i-1][0] + T(i);
s[i][1] = s[i-2][1] + T(i-1);
}
scanf("%d",&tests);
while(tests--)
{
scanf("%lld",&n);
printf("%lld\n",s[n][0] +
s[n][1]);
}
return 0;
}